За функцією залежності х = 50 + 10t - 12t² визначити яка буде швидкість тіла через 5 секунд. Який шлях пройде тіло за 3 c? Замалювати графік залежності швидкості від часу та переміщення від часу.

Дано:

$x=50+10t-12t^2$

$t_1=5\;c$

$t_2=3\;c$

Знайти:  $v(t=5),\;S(t=3),\;v(t),\;S(t)$

Рівняння прямолінійного руху з постійним прискоренням має такий загальний вид:

$x(t)=x_0+v_0t+\frac{at^2}{2}$        (1)

де $x(t),\;x_0,\;v_0,\;t,\;a$ - відповідно координата тіла в момент часу t, початкова координата, початкова швидкість, час, прискорення.

Порівнюємо задане в умові рівняння з рівнянням (1). 

Очевидні висновки:

- початкова координата $x_0=50$ м

- початкова швидкість $v_0=10$ м/с

- прискорення a=-24 $\frac{м}{c^2}$

Швидкість тіла через 5 секунд:   $v=v_0+at_1=10-24*5=-110$ м/с

Звернімо увагу на те, що швидкість початкова була 10 м/с, а стала -110 м/с, тобто змінила не тільки величину (модуль), але і знак. Це означає, що у якийсь момент часу швидкість змінила напрямок, тобто тіло рухалось спочатку в напрямку, що співпадає з напрямком осі ОХ, потім зупинолось, потім стало рухатись у зворотньому напрямку. 

Знайдем момент часу, коли тіло зупинилося.  

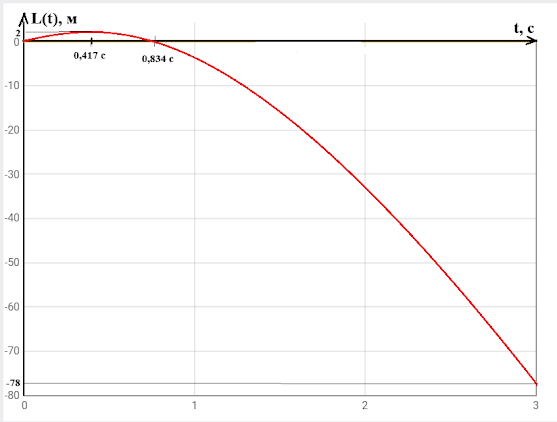
$v_0+at=0$        $10-24t=0$        $t=\frac{10}{24}\approx 0.417$ c

Тіло зупинилося після 0,417 с після початку руху. Знайдемо шлях від початку руху до зупинки. 

$S_1=v_0t+\frac{at^2}{2}=10*0,417-\frac{24*0,417^2}{2}\approx 2,08$ м

Знайдемо шлях тіла у зворотньому напрямку від моменту зупинки до часу t=3 секунди. 

$S_2=\frac{at^2}{2}=\frac{24*(3-0,417)^2}{2}\approx 80,06$ м

Весь шлях за 3 секунди   $S=S_1+S_2=2,08+80,06=82,14$ м

Побудуємо графіки.

Ваш відгук, коментар або лайк дуже важливий для підтримки сайту. Не пошкодуйте 10 секунд свого часу. Не зрозуміли - запитуйте, поясню. Потрібна допомога - пишіть на ivankonosovskiy@gmail.com Допоможу безкоштовно